Normal distributions become more apparent (ie perfect) the finer the level of measurement and the larger the sample from a population You can also calculate coefficients which tell us about the size of the distribution tails in relation to the bump inExample 1 Sketch the gradient, and use that to draw the level curves, of the function ( ) We begin by finding the gradient 〈 〉 Since the function is explicit, we need only concern ourselves here with the derivatives for x and y At this point, we could choose a series of points that mark out a grid for our plane and begin to draw You can't find the tangent line of a function, what you want is the tangent line of a level curve of that function (at a particular point) $\endgroup$ – Hans Lundmark Sep 3 '18 at 549 Example regarding the LowenheimSkolem theorem (from Enderton's Logic)

Calculus Iii Functions Of Several Variables
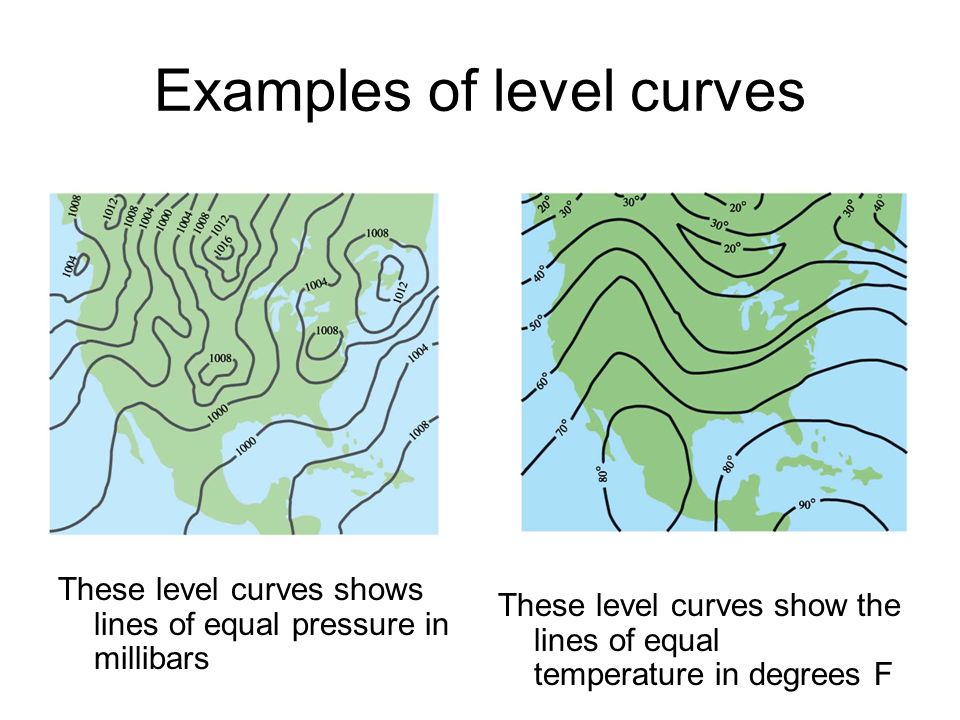
Level curves examples
Level curves examples-Likewise, rv6= 0 Thus, the gradients are not zero and the level curves must be smooth Example 55 The gures below show level curves of uand vfor a number of functions In all cases, the level curves of uare in orange and those of vare in blue For each case we show the level curves separately and then overlayed on each otherOf level curves for the levels k n If the distance in the (x;y) plane between level curves for levels k n and k n 1 is large near a point P on the k n level curve, then the graph is not very steep there However, if the level curves are close together near P, then the graph is steeper near P Can you
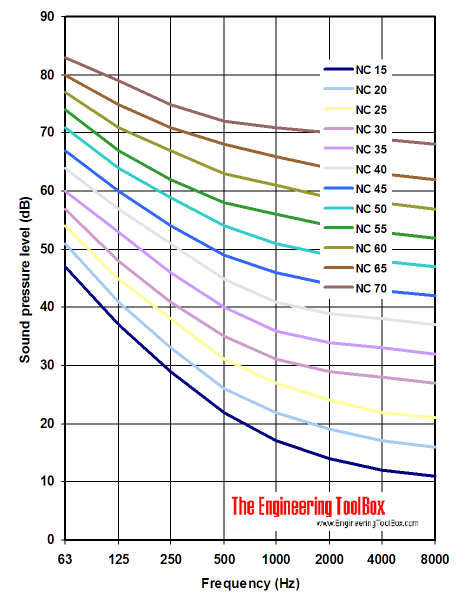



Nc The Noise Criterion
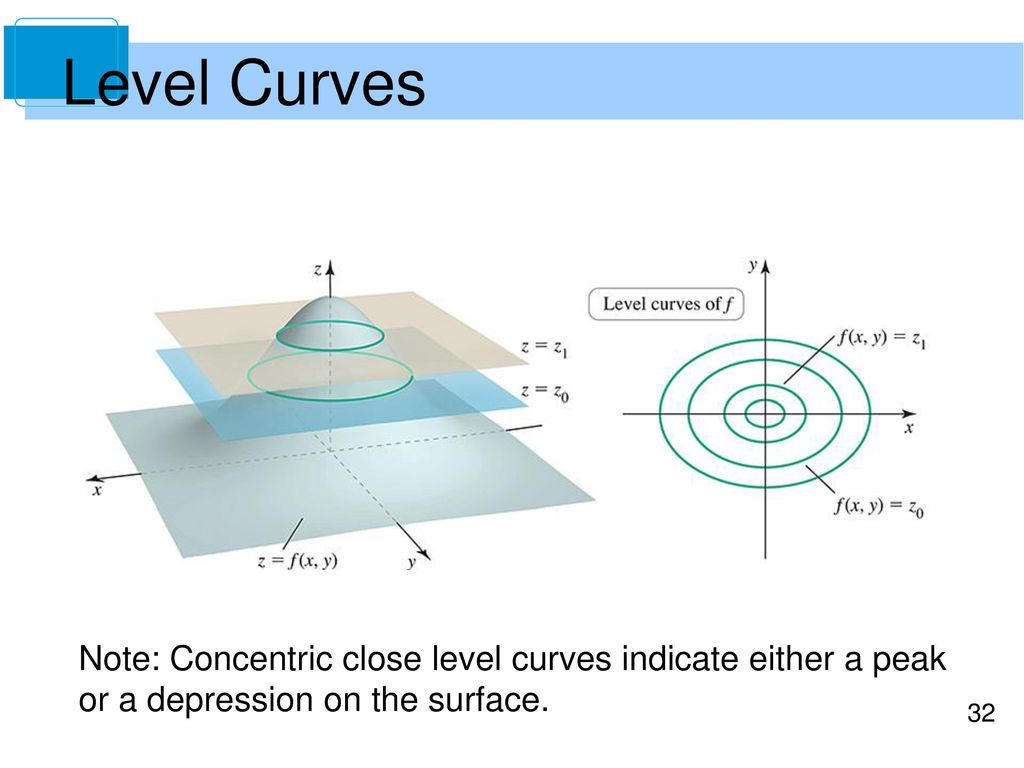
Level Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set Its graph is shown below From the side view, it appears that the minimum value of this function is around 500 Example 4 f (x,y)=2e (x1)2y2 3e (x2)2 (y1)2 2e (x1)2 (y2)2 A level curve of a function f (x,y) is a set of points (x,y) in the plane such that f (x,y)=c for a fixed value c Example 5We have done this in Example 4 at level curves Unfortunately, sometimes it is not possible to rewrite the level curve Unfortunately, sometimes it is not possible to rewrite the level curve However, even in that case we can determine the slope of the tangent line to the level curve by the use of the following rule
Perpendicular to the Level Curve TheoremThe gradient isalways perpendicular to the level curve through its tail Proof We will only show this for a surfa ce z f(x,y) whose level curve c f(x,y) can be parameterized by(x(t),y(t)) Then atangent vector on the level curve can be described by (x'(t),y'(t)) ff Next, the gradient is f(x,y) , xyThe AD curve relationship between the price level and real GDP demanded, holding everything else constant A change in the price level not caused by a component of real GDP changing results in a movement along the AD curve A change in some component of aggregate demand, on the other hand, will shift the AD curveThis Service Has Been Retired Faculty profile information has been migrated to UMassD Sites and the University's Directory
In your first example, the proper solution is $$y=\pm \sqrt{kx^2}$$ You left out the plusorminus That is not a small thing there are usually two values of $y$ for each $x$, and that greatly affects the plotting of the curvesU(x;y) = cas the curve which represents the easiest walking path, that is, altitude does not change along that route The altitude is conserved along the route, hence the terminology conservation law Other examples of level curves are isobars and isotherms An isobar is a planar curve where the atmospheric pressure is constant An isotherm is a planar curve along which the temperature isLevel Curves We have a multivariable function (more than one variable) that is a square root function A level curve is a twodimensional curve got by equating a constant value to the function




Solved Multivariable Functions And Level Curvesi M Having A Chegg Com




Plotting Using Contour In Python Epythonguru
For example, when c 1= 0, the level curve is which is a circle of radius 8 27 Figure 1310 shows the nine level curves for the hemisphere cont'd Figure 1310 Example 3 – Solution 28 One example of a function of two variables used in economics is the CobbDouglas production functionWhen we talk about the graph of a function with two variables defined on a subset D of the xyplane, we mean zfxy xy D= (, ) ,( )∈ If c is a value in the range of f then we can sketch the curve f(x,y) = cThis is called a level curve A collection of level curves can give a good representation of the 3d graphA level curve in R2 is a set of points C= f(x;y) 2R2 jf(x;y) = cg Example 11 The unit circle x2 y2 = 1 can be described as a level curve by being the zero set of f(x;y) = x2 y2 1 Level curves in higher dimension such as R3 require more de ning equations Example 12 The xaxis in R3 is described as a level curve by C= f(x;y;z) 2R3 jy= 0



Ucm Gravity
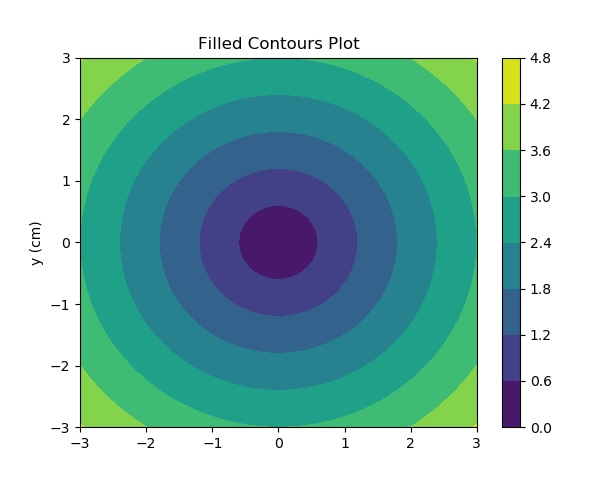



Matplotlib Contour Plot
It looks much like a topographic map of the surfaceA level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve of points (x,y) ,where function have constant value Can be better understood by an example Find the level curves of heights CIn the simplest case, = 2 2, an intersection of this surface with a plane =𝑘 forms a level curve that is a circle Thus, the contour map of this paraboloid will be concentric circles centered at the origin The paraboloid = 2 2 intersected by this surface with a plane =𝑘 forms a circle




Math 15 Lecture 7 Level Curves And Contour Plots Oneclass
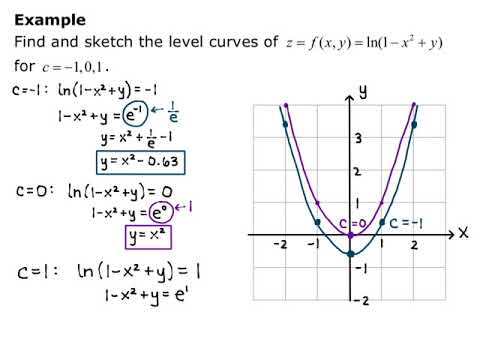



Section 13 1 Level Curves Youtube
The level curves f(x,y) = k are just the traces of the graph of f in the horizontal plane z=k projected down to the xyplane Figure 1 Relation between level curves and a surface k is variating acording to 5015 One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation of theLevel curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant For example the curve at height z = 1 is the circle x2 y2 = 1 On the graph we haveFor example, "tallest building" Search for wildcards or unknown words Put a * in your word or phrase where you want to leave a placeholder For example, "largest * in the world" Search within a range of numbers Put between two numbers For example, camera $50$100 Combine searches Put "OR" between each search query For example, marathon



Problem On Gradient Directional Derivative And Level Curves Leading Lesson
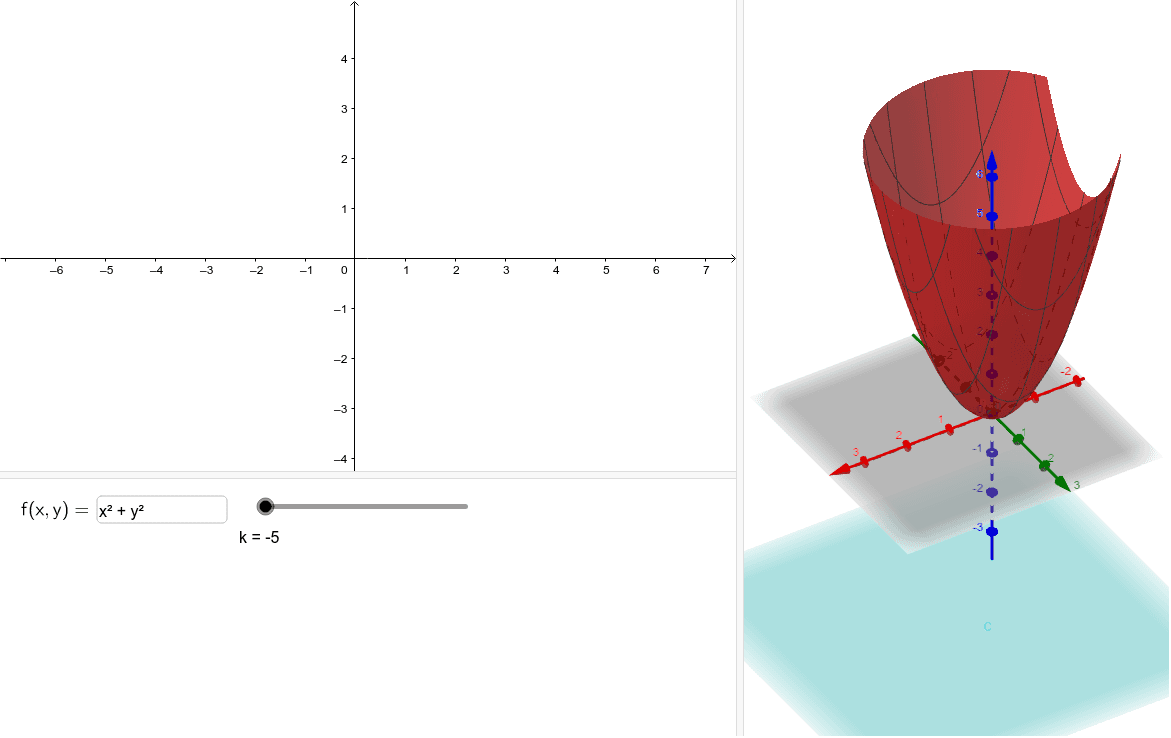



Level Curves Geogebra
R251pdf Curves in R2 Graphs vs Level Sets Graphs(y = f(x The graph of f R \u2192 R is(x y \u28 R2 y = f(x Example When we say \u1cthe curve y = x2,\u1dFigure 10 Contour Plot with Highlighted Level Curve 52 Example 2 Contour Plot for z = x 2 9 y 4 This example is a contour plot for a hyperboloid Details for each step are omitted, since they were discussed for example 1 The steps to create the contour plot are Step 1 Define the function z= f(x;y) and solve it for y in terms of x and zExample, the set Sis in R2 This gure also illustrates the fact that a ball in R2 is just a disk and its boundary18 23 An example of in nitely many alternative optimal solutions in a linear programming problem The level curves for z(x 1;x 2) = 18x 1 6x 2 are parallel to one face of the polygon boundary of the feasible region Moreover



Functions Of Several Variables Ximera




Graphs And Level Curves
Examples Graph of the functions Level curves and level surfaces Slide 8 ' & $ % Scalar functions of 2 variables De nition 3 A scalar function fof two variables (x;y) is a rule that assigns to each ordered pair (x;y) 2DˆIR2 a unique real number, denoted by f(x;y), that is, f DˆIR2!RˆIR Comparison Vector valued functions, r IR!IR2 t413 Sketch several traces or level curves of a function of two variables 414 Recognize a function of three or more variables and identify its level surfaces Our first step is to explain what a function of more than one variable is, starting with functions of two independent variablesX y 143 Level Curves and Level Surfaces Look over book examples!!!



S0 3



1
Higher indifference curves represent a greater level of utility than lower ones In Figure 1, indifference curve Ul can be thought of as a "low" level of utility, while Um is a "medium" level of utility and Uh is a "high" level of utility All of the choices on indifference curve Uh are preferred to all of the choices on Now on to the real problem The level curves (or contour curves) for this surface are given by the equation are found by substituting \(z = k\) In the case of our example this is, \k = \sqrt {{x^2} {y^2}} \hspace{025in}\hspace{025in} \Rightarrow \hspace{025in}\hspace{025in}{x^2} {y^2} = {k^2}\ where \(k\) is any numberExamples Consider the 2dimensional Euclidean distance d ( x , y ) = x 2 y 2 {\displaystyle d (x,y)= {\sqrt {x^ {2}y^ {2}}}} A level set L r ( d ) {\displaystyle L_ {r} (d)} of this function consists of those points that lie at a distance of r {\displaystyle r} from the origin, otherwise known as a circle




Applicable Mathematics 2 Examples 1 Level Curves




Level Surfaces
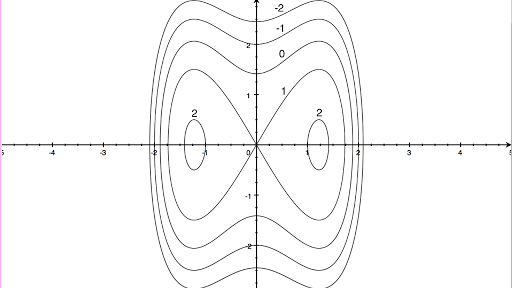
The level curve of this function for the value 2 is empty (there are no values of (x, y) such that f(x, y) = 2) and the level curve for the value 1 is the set all all points (x, y) In less extreme examples, some but not all level curves are sets Consider a basically conical mountain, with terraces at heights of and 40;Example 7 Describe the level curves of the function f(x,y) = x2 y2 from Examples 2 and 3 Answer Figure a shows horizontal cross sections of the graph of f and Figure b shows the corresponding level curves • The level curve f = c is the circle of radius √ c with its center at the origin if c > 0, is the origin if x = 0, and is empty if c < 0 (The surface is called a "circularView Mth254_ExemplarExamples7pdf from MATH 254 at Oregon State University Math 254 Exemplar Examples 7 (1) Below is are several level curves of z = f




Visualizing Surface And Level Curves Youtube




Nc The Noise Criterion
Level Curves The level curves are curves of constant elevation above sea level If you walk along one of these contour lines, you neither ascend nor descend Another common example is the temperature function introduced in the opening paragraph of this section Here the level curves are called isothermals and join locations with the same temperatureLevel Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, the Level Curves and Surfaces Example 3 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set



Usna Edu




Examples Of Level Curves For Different Types Of Functions Calculus Coaches
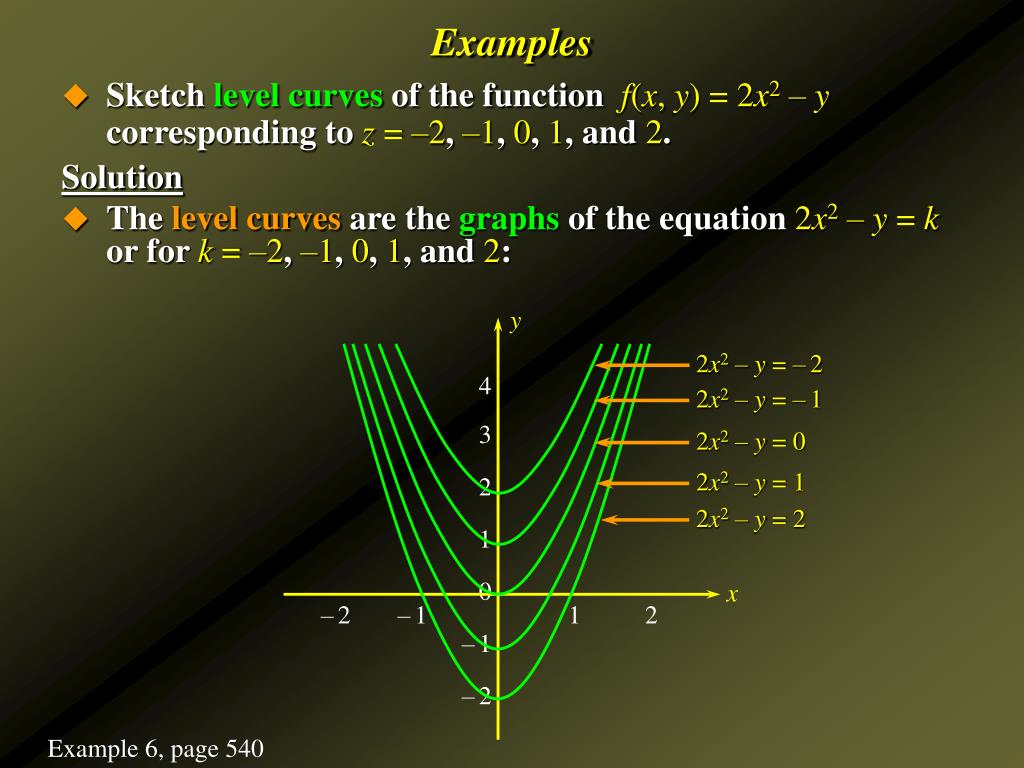
Answer A level curve simply means looking at a three dimensional curve and focussing on those parts at a certain value of z for instance If you look at very detailed maps for example you get the idea of the y and x coordinates which on maps are normally North and South axes Bu as we know theSolution The level curves of are curves in the plane along which has a constant value We now sketch the resulting curves for a couple values of The curve consists of all points satisfying That is, it has points where or Similarly, the and level curves are given by and Hence our sketch of the level curves of looks like Sketch several traces or level curves of a function of two variables The function might map a point in the plane to a third quantity (for example, pressure) at a given time The method for finding the domain of a function of more than two variables is analogous to the method for functions of one or two variables




How To Read A Sea Level Curve Geological Digressions



S0 3
How to Use the Learning Curve Theory (with Examples) The learning curve theory is a way to understand the improved performance of an employee or investment over time The idea is that the more an employee does something, the better they will get at it, which translates to lower cost and higher output in the long termPractice problems Sketch the level curves of Sketch the threedimensional surface and level curves of Consider the surface At , find a 3d tangent vector that points in the direction of steepest ascent Find a normal vector to the surface at the point Give the equation for the tangent plane to the surface at the pointAs in this example, the points $(x,y)$ such that $f(x,y)=k$ usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface;




8 Calculus Of Several Variables U Functions Of
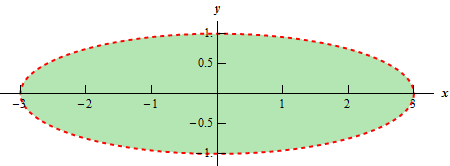



Calculus Iii Functions Of Several Variables
Contour plots, level curves ezcontour, ezplot The function ezcontour plots level curves for functions of two variables z = f(x,y)The second and third arguments are the plotting limits for each of the independent variables x and yOne drawback to ezcontour is that it does identify the contour levels Adding a colorbar to the graph will give you an approximate idea of the level associatedFree ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics and



Reading Aggregate Demand Macroeconomics
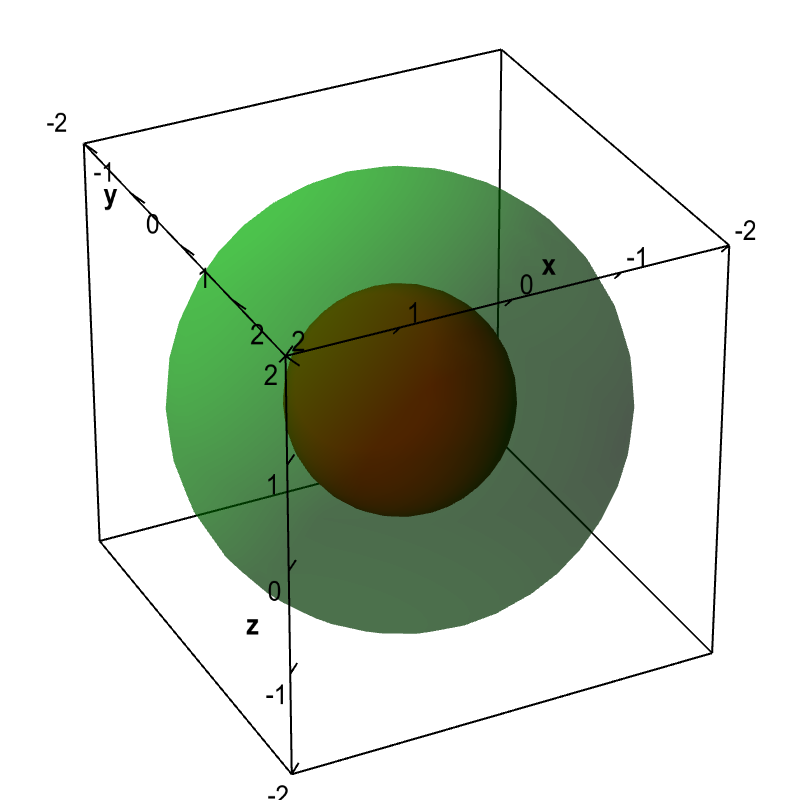



Level Set Examples Math Insight



Level Curves And Contour Plots Mathonline




Level Set Wikipedia



Relief Functions And Level Curves




Level Curves




Level Curves




Level Sets Ximera




Level Set Examples Math Insight



Level Curves And Contour Plots Mathonline



1




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Level Curves



1



Relief Functions And Level Curves




Calculus Iii Functions Of Several Variables
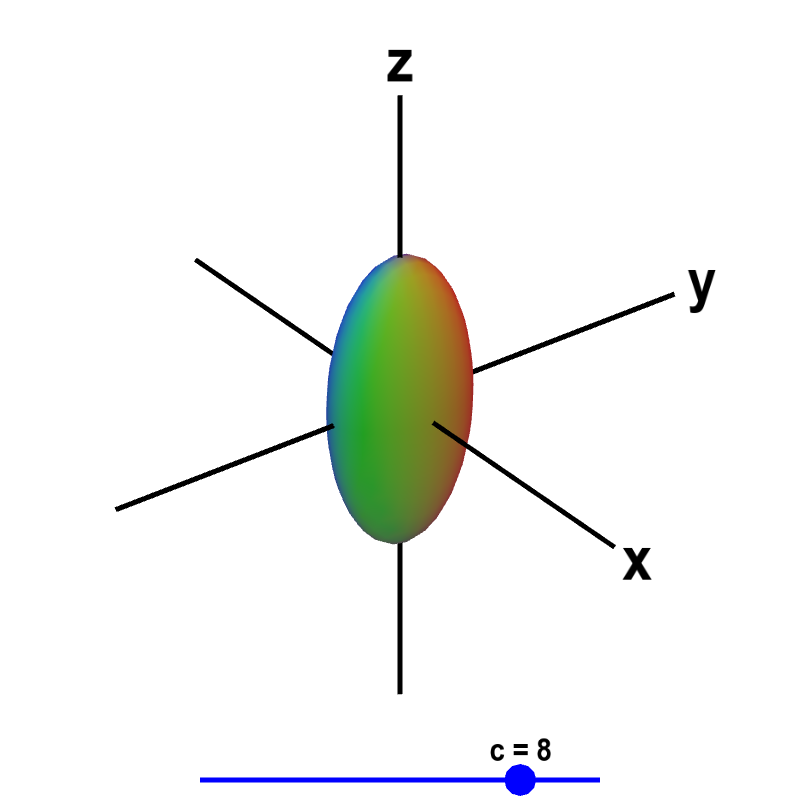



Level Sets Math Insight



S0 3



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero




Level Set Examples Math Insight
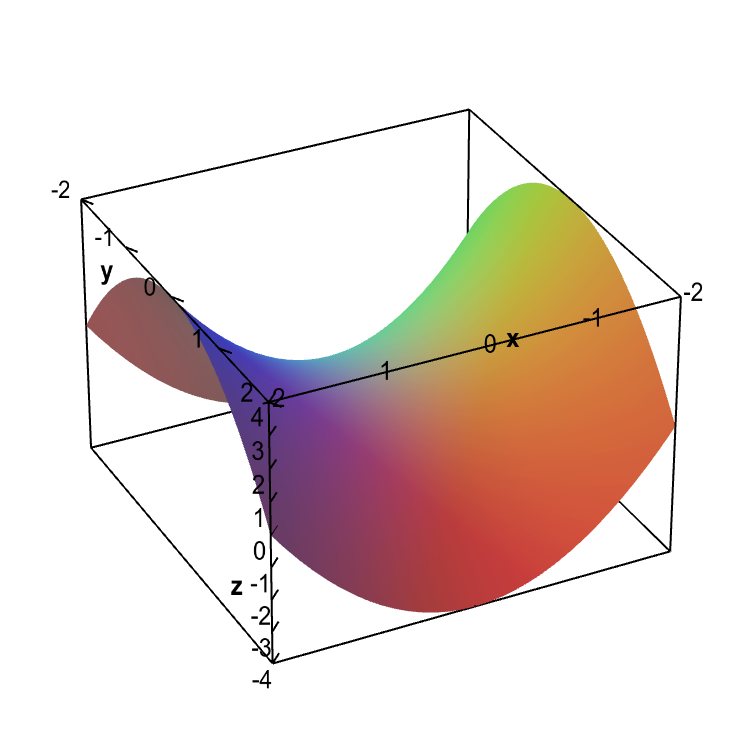



Level Set Examples Math Insight




Calculus Iii Functions Of Several Variables



Extra Explanation Wiskunde Op Tilburg University




Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram




Introduction To Functions Of Several Variables Ppt Download
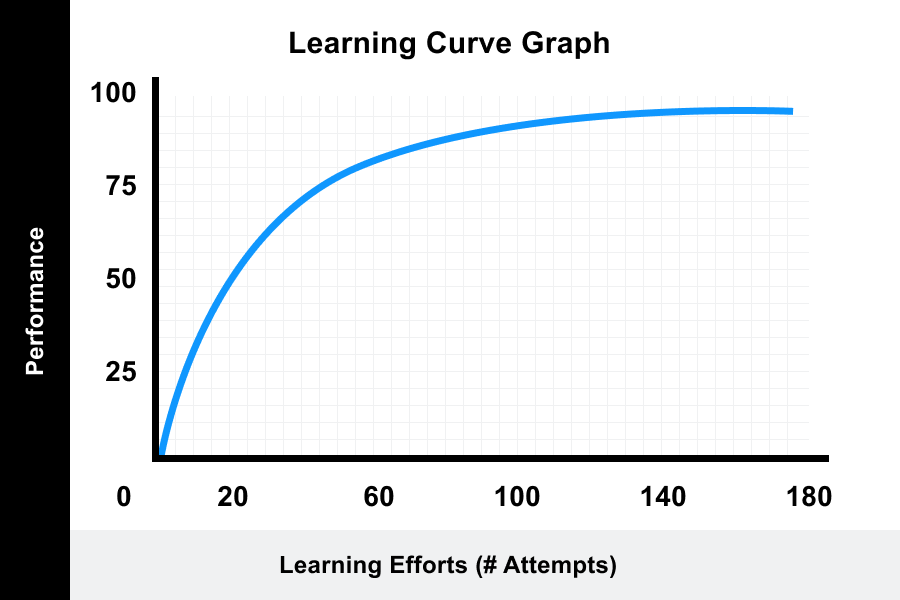



Learning Curve Theory Meaning Formulas Graphs



Level Curves And Contour Plots Mathonline
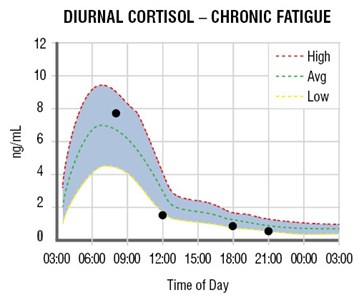



Diurnal Cortisol Curves




How To Sketch Level Curves Youtube




Level Sets Math Insight




Solved Example 11 Sketch The Level Curves Of The Function Chegg Com
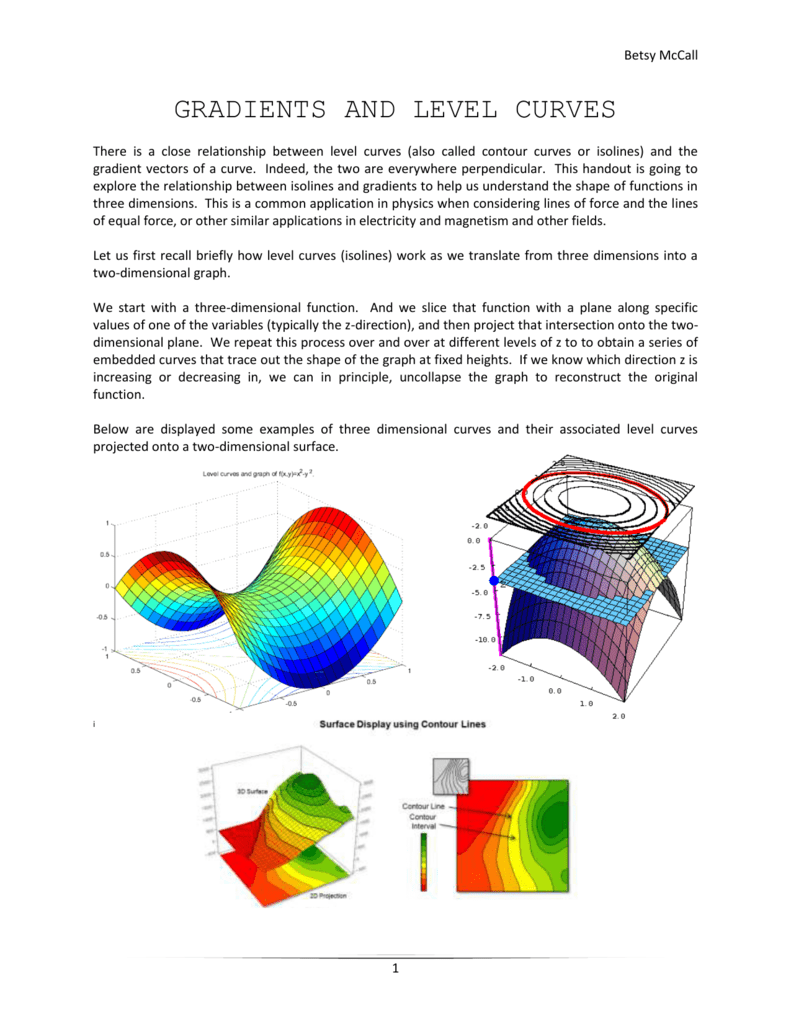



Gradients Level Curves




Matb41h3 Midterm Detailed Examples For Drawing Level Curves Oneclass




Solved In Calculus I And Ii We Worked With Functions Chegg Com




Solved 3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com
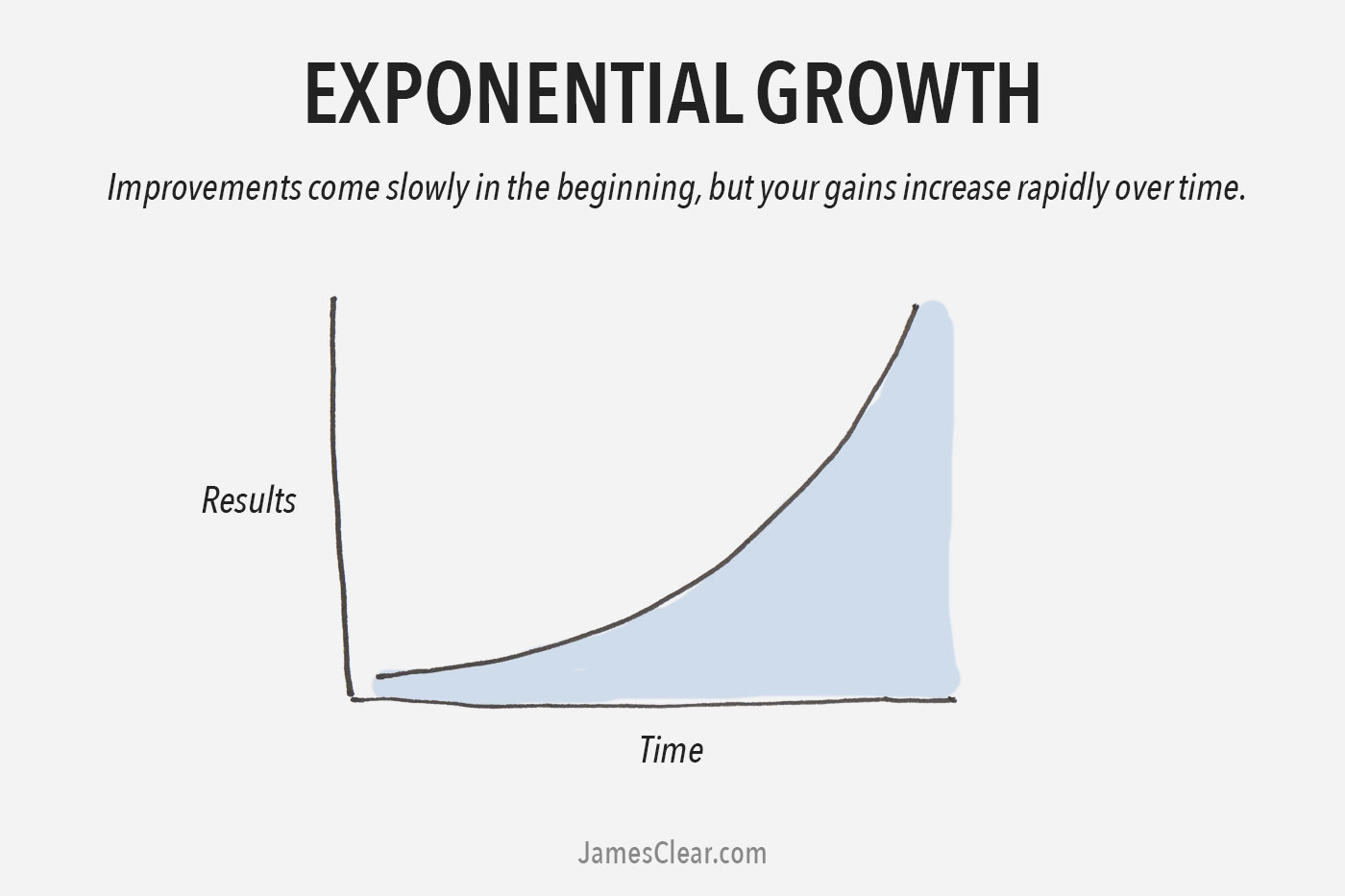



The 2 Types Of Growth Which Growth Curve Are You Following




Level Sets Math Insight
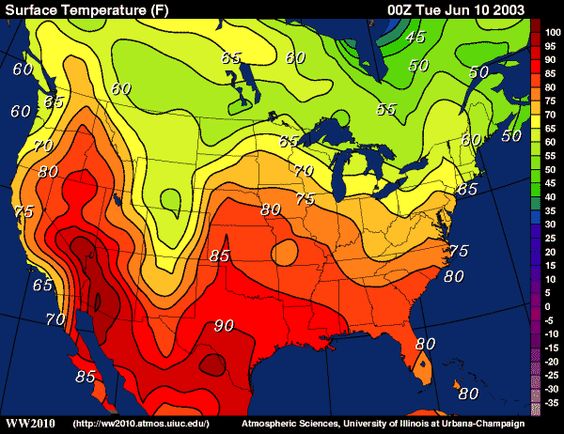



Level Sets Ximera




How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube




Level Surfaces




Level Curves R Calculus




Calculus Iii Functions Of Several Variables




Level Curves Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Curves Examples Done In Mathematica Last Modified Spring 14




Level Set Wikipedia



Math 225 Calculus Iii




Level Sets Math Insight




Solved Describe The Level Curves Of The Function Z 8 2x 7y Chegg Com



Contour Maps Article Khan Academy



1




Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram




Calculus Iii Functions Of Several Variables




Two Examples Of Eustatic Sea Level Curves That Show Significant Download Scientific Diagram




Level Set Wikipedia



Making Difficulty Curves In Games Stuff Made By Dave



Ams Sunysb Edu




Relation Between Level Curves And Horizontal Traces Tex Latex Stack Exchange




Fun Math Art Pictures Benice Equation Scilab Example Plotting Implicit Curves Level Curves



Usna Edu



Math 225 Calculus Iii




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Set Wikipedia




Level Curves Of Functions Of Two Variables Youtube




Level Curves And Cross Sections Maple Help




Applicable Mathematics 2 Examples 1 Level Curves




How To Sketch Level Curves Vector Calculus Youtube



Elementary Calculus Example 5 Same Of Hyperbolic Paraboloid




Level Curves Example 1




Level Curves Of The Error Function Download Scientific Diagram
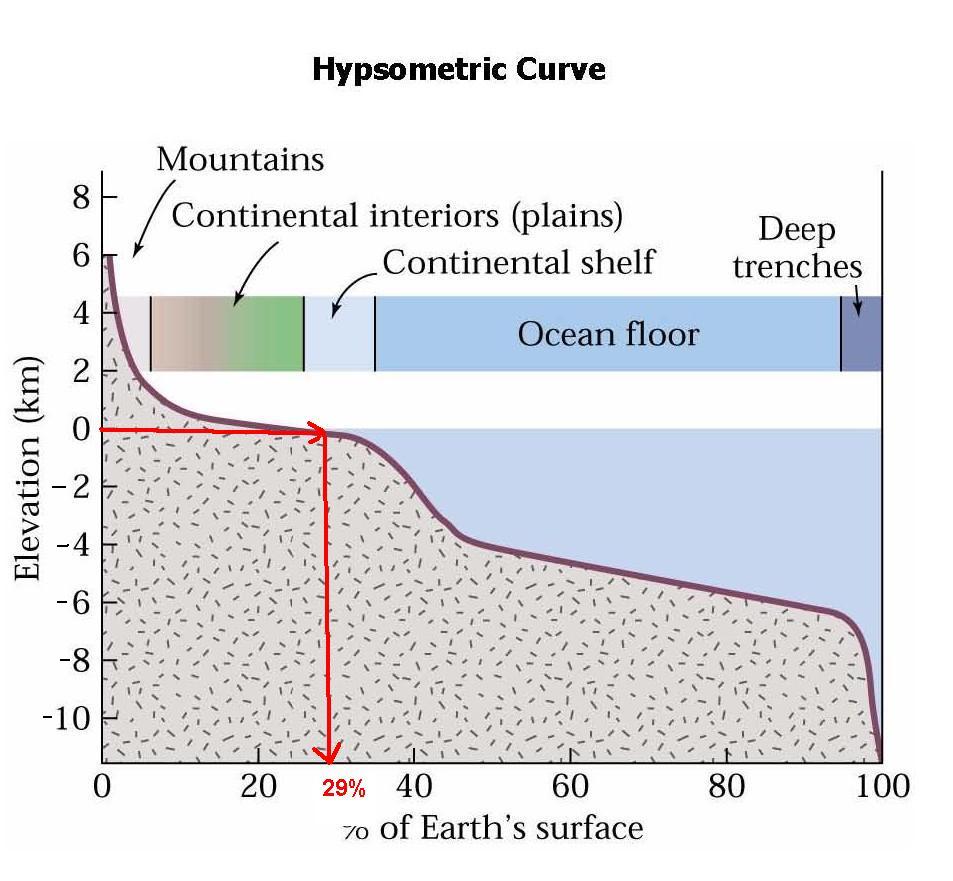



Hypsometric Curve




Solved Points Writing Prompt Typed 100 0 Words Eyouitown Words Define The Level Curves Of A Function Of Two Variables Describe How Level Curves Can Help You Sketch A Graph Of A Surfacea Examples
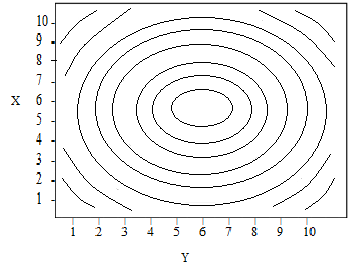



Contour Plots Definition Examples Statistics How To



The Gradient And Directional Derivative




Unit 5 Functions Harvard Knill Teaching Summer19 Handouts Weeآ Unit 5 Functions Lecture 5 1 Pdf Document




Level Curves In Mathbb R 3 Mathematics Stack Exchange
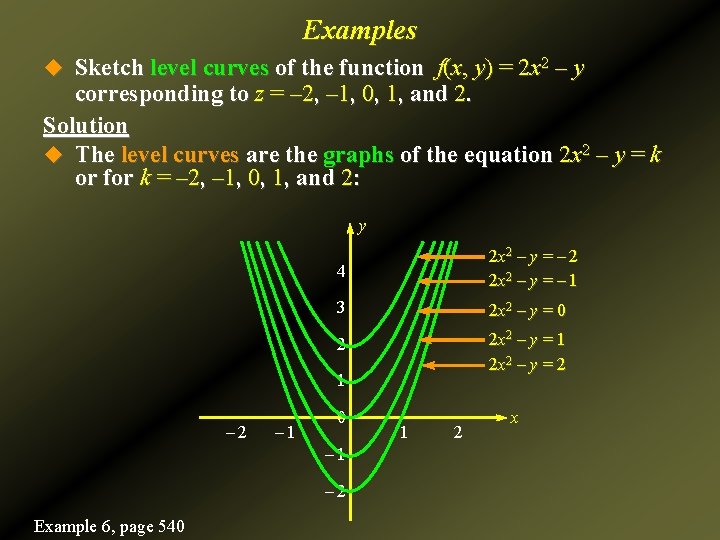



8 Calculus Of Several Variables U Functions Of




Level Curves Examples Done In Mathematica Last Modified Spring 14



Introduction To Functions Of Several Variables Ppt Download



Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id



Ocw Mit Edu


