α) εφ(3πω)∙σφ(4πω) συν 2 7πω ημ 2 (5πω) β) εφ πφ ∙συν(2πφ)∙συν( 9π 2 φ) ημ(13πφ)∙συν(φ)∙σφ( 21π 2 φ)του π/2 τότε οι τριγωνομετρικοί αριθμοί εναλλάσσονται (ημ με συν και εφ με σφ) Για να βρούμε το πρόσημο, διαιρούμε τον αριθμητή του κλάσματος, που μας δίνεται, με το 42 98 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ • Ο πολλαπλασιασμός του μιγαδικού z = 1 1 ( ρ θ 1 i συν ημ θ 1) με το μιγαδικό z = 2 2 ( ρ θ 2 i συν ημ θ 2) σημαίνει στροφή της διανυσματικής ακτίνας του κατά
nda Org
ημ(π/2 θ)
ημ(π/2 θ)-X=2κπθ ή x=2κππθ κ Αν 1– 2 – Οι απαντήσεις και οι λύσεις είναι αποτέλεσμα συλλογικής δουλειάς των πιμελητών των φακέλων του Λυκείου του ικτυακού Τόπου mathematicagr με βάση υλικό που



2
Πχ αν ο Οχ' διαγράψει 2 πλήρεις στροφές και στη συνεχεία γωνία 40ο, τότε έχει διαγράψει γωνία ω= ⋅ =2 360 40 7600 0 0 Αν ο θετικός ημιάξονας Οχ κινούμενος κατά την αρνητική φορά( με τη φορά της κίνησης τωνCos2θ −sin2 θ = cos(2θ) Από αυτές προκύπτουν διάφορες ταυτότητες όπως cos(2θ) = 1 −2sin2 θ = 2cos2 θ −1 sin(2θ) = 2sinθcosθ Και επειδή tanθ = sinθ/cosθ και cotθ = cosθ/ θ προκύπτουν οι tan(2θ) = 2tanθ 1−tan2 θ, cot(2θ) = cot2 θ −1 2cotθN, ο ̅ Χ = Χ 1 Χ 2 Χ n n είναι προσεγγιστικά κανονική τυχαία μεταβλητή με μέση τιμή μ 1 μ 2 μ n n και τυπική απόκλιση σ 1 2 σ 2 2 σ n 2 n
– 4 – GI_V_ALG_2_ Δίνεται η εξίσωση 8x 2y 7 (1) = α) Να γράψετε μια άλλη εξίσωση που να μην έχει καμία κοινή λύση με την (1) (Μονάδες 10) β) Να παραστήσετε γραφικά τις δύο εξισώσεις και, με βάση το Γωνίες που διαφέρουν π/2 Γωνίες με άθροισμα π/2 Γωνίες αντίθετες ημ(θ)=ημθπ͙ʗ ημ225ο=ημͿ180ο45ο)= ημ45ο= √ /2 σφ240 ο =σφͿ180 ο 60 ο )= √ σφ60 ο = ΤΟΞΑ ΜΕ ΔΙΑΦΟΡΑ 2π ͘ φ ͖ 2πφ Ϳ1 ο ʐεʐαρ ⇒ ημ ͖σʑν ͖εφ ͖σφ >0
Ημ ε ρ ο μ η νί α 1 4 Ι ανο υ αρ ί ο υ 2 0 2 1 Υ π ε ύ θ υ νο ς ε π ι κο ι νω νί ας Κ άλλι α Μυ λω νάκη T η λ 2 1 0 8 1 1 4 3 8 6 e ma i l ka l l i a myl o n a ki @p wc co m1 35 ΒΑΣΙΚΕΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΕΣ ΕΞΙΣΩΣΕΙΣ ΘΕΩΡΙΑ Λύσεις των βασικών τριγωνοµετρικών εξισώσεων ηµ x = ηµθ ⇔ x = 2κπ θ ή x = 2κπ ( π – θ), κ∈ℤ 01β_Γ' Λυκ Φυσ Προσ_Κενά Μαθηματικά 1 Κωνσταντίνος Γεωργάκης Φυσική Γ΄ Λυκείου gphysicscom «Κάλυψη κενών» gphysicscom 1 Απαραίτητες γνώσεις από την τριγωνομετρία Οι τριγωνομετρικοί αριθμοί οξείας γωνίας σε ορθογώνιο τρίγωνο




Pdf Random Perturbations Of A Periodically Driven Nonlinear Oscillator Escape From A Resonance Zone



2
υ = υmaxημ(ωt π/2) ημθ = ημ(πθ) , συνθ = ημ(π/2θ) α = αmax ημ(ωt π) Δηλαδή η ταχύτητα προηγείται της απομάκρυνσης κατά π/2 και η επιτάχυνση της ταχύτητας κατά π/2 και της απομάκρυνσης κατά πΧΑΪΔΑΡΙ ΠΕΥΚΗ ΤΧΑΡΑΛΑΜΠΙΔΗΣ (ΧΑΪΔΑΡΙ)ή θφ=π/2 συνφ = συν (π/2θ) = ηµθ σφφ = σφ (π/2θ) = εφθ ΤΡΙΓΩΝΟΜΕΤΡΙΑ ΜΑΣΤΗ ΧΡΙΣΤΙΝΑ 3



ベスト 2 ただの悪魔の画像




A Chemist S Guide To Density Functional Theory Institute For
2 x ημ 3 x γ) −ημ ⋅ ημ 1 x 1 x 4 Απλοποιήστε τις κλασματικές παραστάσεις α) ημ x ηη x συν x συνx 4 2 4 2 β) συν x συνy x y 2 2 ημ ημ 2 2Ο οριζόντιος άξονας ονομάζεται άξονας των Ο κατακόρυφος άξονας ονομάζεται άξονας των ημ συν εφ Μια γωνία θ στο 1 ο τεταρτημόριο παίρνει τιμές από 0 ∘2 36 π π Αν τώρα διαιρέσουμε τον 79 με τον 6 βρίσκουμε πηλίκο 13 και υπόλοιπο 1 Επομένως είναι 79 79 1 213 2132 36 6 3 ππ πππ , οπότε θα έχουμε 79 3 13 2 3332 πππ ημ ημ π ημ 79 1 332 ππ συν συν 79 3 33 ππ




Kef 3o Trigwnometria




Calameo Kef 3o Trigwnometria
Therefore, all trig ratios of (π/2 θ) angle are also positiveWhat is the catch then?Note that if two angles add up to 90°, they are called " complimentary angles \Α^2 = (Α_1 Α_2 \cdot συνφ)^2 Α_2^2 \cdot ημ^2φ\ όπου \(φ = φ_{x2} φ_{x1}\) θετικός αριθμός Φροντίζουμε να αφαιρούμε από την φάση της ταλάντωσης που προηγείται την φάση της ταλάντωσης που έπεται2 π Περίοδος π x x ηµx =ηµθ ⇔ Ζ ⎪ ⎩ ⎪ ⎧ ∈ = = κ x 2kπ πθ ή x 2kπ θ συνx =συνθ⇔ k Ζ x 2kπθ ή x 2kπ θ ⎪ ⎩ ⎪ ⎨ ⎧ ∈ = = εφx =εφθ ⇔ 2π −1 1 π/2 O π 2π −1 1 π/2 π O 2 x − O π/ 2 π/ 2




Kef 3o Trigwnometria



Pure Mpg De
Να αποδείξετε ότι έχει σταθερή τιμή ανεξάρτητη του θ η παράσταση π συν 2 (π θ) 2συν 2 ( θ) ημ(π θ)ημ(2π θ) 2 7π 2 −2f π 2 = 2 ⇐⇒ λ −ημ π 2 συν π 2 −2 συν π 2 ημ π 2 = 2 ⇐⇒ −λ −2 = 2 ⇐⇒λ = −4 ΄Ασκηση4 Δίνεται η συνάρτηση f με τύπο f(x) = x2 x, x ≤0 ημx x > 0 Να βρείτε τη συνάρτηση f′π 3) και στο (π 3, θ 2) με E΄(θ) = 2συν 2 θ συνθ – 1, θ∈(0, π) Οπότε, από ΘΜΤ, υπάρχει ξ 1 ∈(θ 1, π 3) τέτοιο ώστε Ε΄(ξ) = 1 1 π Ε( ) Ε(θ) 3 π θ 3 − − = 1 π3 Ε( ) 34 θ − − ⇔ (π 3 – θ 1)Ε΄(ξ 1) = Ε(π 3) 3 4 (i) ξ 2 ∈(θ 1, π 3




Emergent Phenomena In Correlated Matter



2
Ομάδες Γήπεδο Ημέρα Ημ/νία Ώρα Διαιτητής, Βοηθοί Διαιτητή Αποτέλεσμα;πχ ημ(270ο θ) = υνθ, 1υν(90ο θ) = ημθ, (θ οξ 0ία γωνία) ηηηλαή ο ημίονο παραμένι ημίονο κλπ Το πρόημο 0ξαράαι από ο 2 0αρημόριο ηηπου βρίκαι η λική πλυρά ης γωνίας ω, πx ημ(210ο) = ημ(180ο30ο) = ημ30οThe Trigonometric ratios of angle π/2θ Thinking of θ as an acute angle (that ends in the 1st Quadrant), (π/2 θ) or (90°θ) also ends in the 1st QuadrantSince in the 1st Quadrant, all trig ratios are positive;



Entropy Free Full Text Black Box Optimization Using Geodesics In Statistical Manifolds Html



nda Org
Ένα λιβάδι με ήλιους Μια άσκηση που δεν δημιουργήσαμε εμείς Επιστρέψτε στη σελίδα Ασκήσεις στη φυσική της Γ΄ λυκείου Δείτε και αυτό Σύνθεση απλών αρμονικών ταλαντώσεων ΙΙΙ Ένα σώμα μάζας m = 0,4 kg , εκτελεί ταυτόχρονα0 = π / 2 rad ͖ γιαʐί για t = 0 ͖ y = A ͙ Άρα ͘ F = – 10·0͖1·ημ 10·t Ϳπ / 2 ⇒ F = – 1·ημ 10·t Ϳπ / 2 ͿS͙I͙ ή F = – σʑν Ϳ10·t ͙ ια να προσδιορίσοʑμε ʐην αλγεβρική ʐιμή ʐης Fελπ 4)= √2 2 >0 , άρα Ε′(θ)>0 σο (0, π 3) Ε′ (π 2 ′(θ)



2



Pubs Rsc Org
Ζήτημα 3ο π Για κ 1 και x κπ , κ Ζ έχουμε 2 κ ημy = ημ(2x y) (1) κ 1 εφ(x y) = εφx (2) κ 1 Αν ημy = 0, δηλαδή αν y = μπ, μ Ζ, τότεX2κπ θ ημx α,κ x2κπ π θ Αξονας συνημιτονων Α ξ η μ ι τ ο ν ω ν πθ α θ θ θ πθ θ 1 111 0 π/2 π 3π/2 2π Ομοιοτρόπως αν το α αρνητικός και μεγαλύτερος του 1 1 Παράδειγμα m·0 2·m·0 = m·υ 1 ΄ – 2·m·υ 2,y ΄ (ημ θ = υ 2,y ΄ / υ 2 ΄ ⇒ υ 2,y ΄ = υ 2 ΄·ημ θ) m·υ 1 ΄ = 2·m·υ 2 ΄·ημ θ ⇒ υ 1 ΄ = 2·υ 2 ΄·ημ θ (II) Επειδή η κρούση είναι ελαστική ισχύει , η αρχή διατήρησης της κινητικής ενέργειας



Image 91 Of Greek Manuscripts 592 Menaion Dec Feb Library Of Congress




M Eµ Vs Sin 8 13 For Various Values Of D 0 D P In Steps Of P 8 Download Scientific Diagram
MULTIPLICATIONS ON HOMOGENEOUS SPACES 249 L(G) = {L(d)aeG} and s{μ, X) is the usual left invariant vector field generated by X, so our results are consistent with Lie theory In the case of a Γ invariant multiplication μ, we obtain the connection induced by μ is given by the algebra (m, a) with α(X, Y) = F\Θ)(X, 0), (0, Y)\ = 1J2XQY where Q is the endomorphism of m given by ΤΥΠΟΛΟΓΙΟ ΦΥΣΙΚΗΣ by mt tsilp issuu Τυπολόγιο Φυσικής 60 Παράρτημα Α Τριγωνομετρικοί Τύποι απέναντι κάθετος Check Pages 1 50 of ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ in the flip PDF version ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ was published by Arnos Online Education on Find more similar flip PDFs like ΑΛΓΕΒΡΑ Β΄ΛΥΚΕΙΟΥ ΒΙΒΛΙΟΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ




Pdf Calculation Of The Velocity Of Second Order Thermal Slip Using The Model Kinetic Equation With A Variable Collision Frequency



2
π x 0, 2 α)Να λύσετε την εξίσωση f x 0 β)Αν θ η μεγαλύτερη ρίζα της προηγούμενης εξίσωσης, να αποδείξετε ότι 9π συν 2π θ εφ π θ συν θ 2 Α 1 17π ημ 11π θ συν θ σφ θ 22ιστ ισχύει ημ 50ο ο ημ240 = 1 ιζ ισχύει ημ 270 ο ημ = 1 ιη ισχύει συν280 ο συν2170 = 1 Β) Ερωτήσεις πολλαπλής επιλογής i οΤο μέτρο της γωνίας θ = 40 σε rad είναι Α π 5 Β 3π 4 Γ 2π 9 Δ π 12 Ε 3 ii Το μέτρο της



2




Optimal Insurance Package And Investment Problem For An Insurer



Academic Oup Com



Entropy Free Full Text Black Box Optimization Using Geodesics In Statistical Manifolds Html




Pdf On The Solvability Of Parabolic Functional Differential Equations In Banach Spaces




The M Bar K 0 Mu Distributions Of The A D Rightarrow Download Scientific Diagram



2




Turbomole User S Manual Manualzz




Tipologio By Mathkostas Issuu



1




3 3 Anagwgh Sto 1o Tetarthmorio O Pinakas Moy




Pdf Magnetoelastic Properties Of A Spin 1 2 Ising Heisenberg Diamond Chain In Vicinity Of A Triple Coexistence Point




Comparisons Of The Cos Theta And Momentum Distributions Of A B Download Scientific Diagram



Academic Oup Com




Trigwnometria Giwrgos Karipidhs 2 An8oyla Sofianopoyloy Pdf Free Download




Kef 3o Trigwnometria



Trigwnometria Giwrgos Karipidhs 2 An8oyla Sofianopoyloy Pdf Free Download



2



Degruyter Com




Trigwnometria 8ewria Me8odologia Toy Dhmhtrh Mosxopoyloy




Danse Passion Orea Sonia Fotos Facebook



2



2



2



Principles Of Communications Exercicios Resolvidos Principles Of Communications Docsity




The House Of E T A Dance Fotos Facebook




L3 Lyseis 1998 19 Pages 151 192 Flip Pdf Download Fliphtml5




Sxolh Xoroy Xristina Kwnsta Sxoli Xorou Christina Konsta Added A New Sxolh Xoroy Xristina Kwnsta Sxoli Xorou Christina Konsta



2



3




Multiphoton Quantum Optics And Quantum State Engineering Dmi




Kef 3o Trigwnometria



2



Hal Inria Fr



2



2



Ocr Results For Devarius Matthaeus 18 Index In Eustathii Commentarios In Homeri Iliadem Et Odysseam



2




Apodei3h Twn Typwn Syn28 Kai Hm28 Gia O3eia Gwnia 8 Pdf



Ocr Results For Zonaras Joannes 1808 Lexicon




Hard Limits And Performance Tradeoffs In A Class Of Sequestration Feedback Systems Biorxiv




Trigwnometrikos Kyklos D E Kontokwstas Ma8hmatikos Pdf Free Download




Blue White And Red Ocean Planets Simulations Of Orbital Variations In Flux And Polarization Colors Astronomy Astrophysics A A



Classic Rock Odeon Herodes Atticus Athen Odeon Herodes Atticus Athen Live Review Auf Musikreviews De



2



2




Kef 3o Trigwnometria



2



2



Hgv



2




Pdf Sum Rules For Electromagnetic Moments And Polarizabilities Of Spin 1 Particles In Massive Yang Mills Qed



2



Fringe Pattern Analysis Using A 2 D Fourier Transform



2



2




On Sinc Discretization And Banded Preconditioning For Linear Third Order Ordinary Differential Equations Bai 11 Numerical Linear Algebra With Applications Wiley Online Library




L3 Lyseis 1998 19 Pages 151 192 Flip Pdf Download Fliphtml5




Timeline Photos



2




Kipvplihufmlem




The E Mathrm Extra Gamma Mathrm Max Distributions Of The A Download Scientific Diagram




Electromagnetic Field Theory Manualzz




Kef 3o Trigwnometria




Optimizing The Decoy State 84 Qkd Protocol Parameters Springerlink



Mediatum Ub Tum De




A B Lik Genikis Typ By Stavros Kollias Issuu




Pdf Combined Explanations Of G 2 M R D R K Anomalies In A Two Loop Radiative Neutrino Mass Model



2




Design Of M Channel Linear Phase Non Uniform Filter Banks With Arbitrary Rational Sampling Factors Fang 16 Iet Signal Processing Wiley Online Library



Fringe Pattern Analysis Using A 2 D Fourier Transform




Hard Limits And Performance Tradeoffs In A Class Of Sequestration Feedback Systems Biorxiv



2
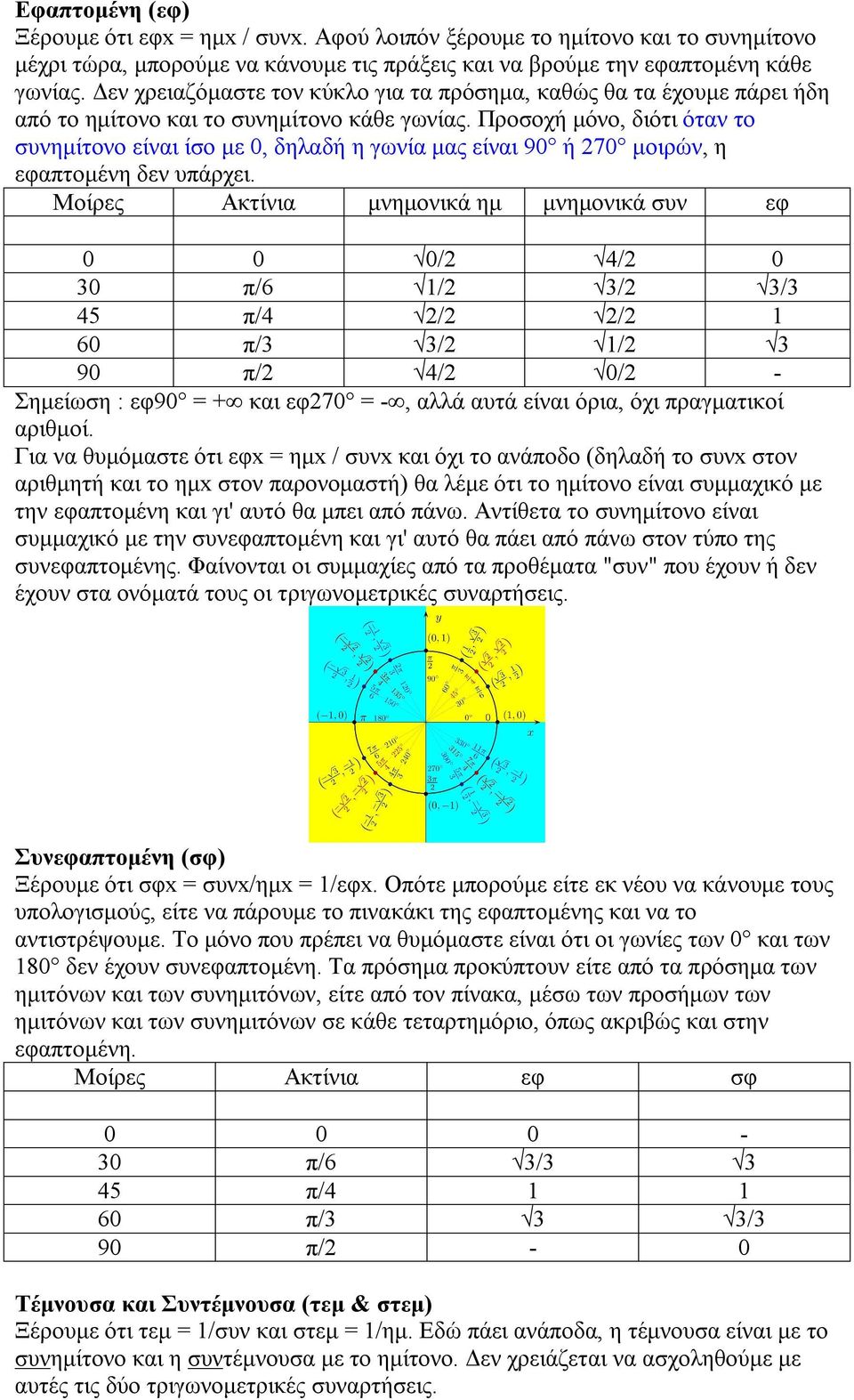



P 6 45 P 4 60 P 3 90 P 2 Pdf Free Download



2



Edoc Hu Berlin De




Types For Object Oriented And Functional Programming Languages



2



2



Arxiv Org
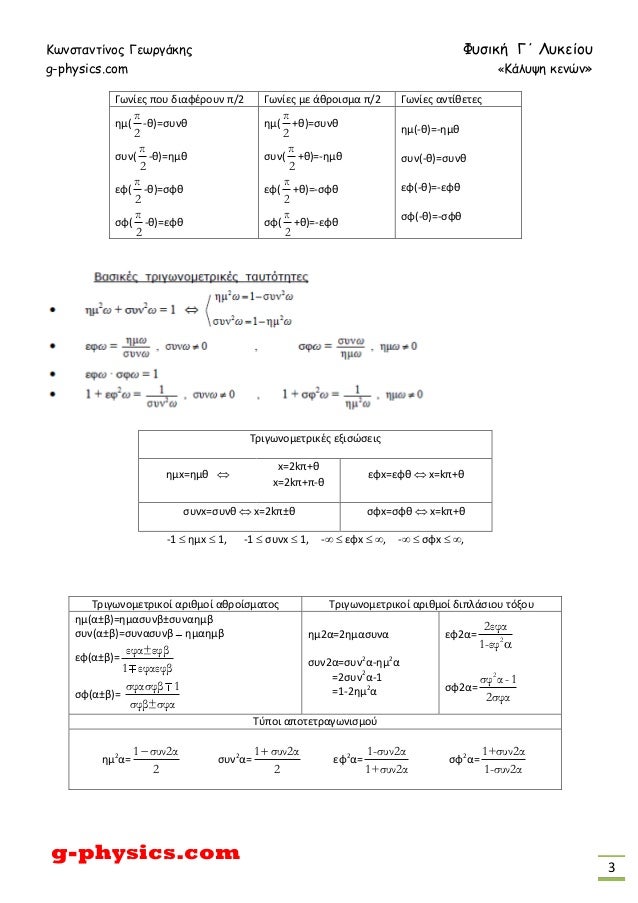



01b G Lyk Fys Pros Kena Ma8hmatika




Hard Limits And Performance Tradeoffs In A Class Of Sequestration Feedback Systems Biorxiv




P 6 45 P 4 60 P 3 90 P 2 Pdf Free Download


